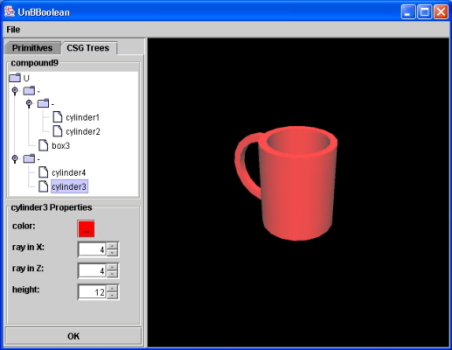
UnBBoolean Author: Danilo Balby UnBBoolean is a 3D modeling tool to apply boolean set operations on primitive solids. It's based on Constructive Solid Geometry concepts. Java3D is required. Includes a library to apply boolean set operations on solids (J3DBool), that can be used by any Java3D app. Download now or visit the project's page on sourceforge.net.

The boolean set operations The boolean set operations are intuitive and popular ways to combine solids based on the set operations. The three main are: Union (u): generates a solid containing all the volume from two other solids. Intersection (n): generates a solid containing the coincident volume from two other solids. Difference (-): generates a solid containing the volume from one solid that is outside from another solid. Due to its simplicity and efficiency, the boolean set operations are commonly used to compose 3D models. They're available on the most of 3D modeling tools nowadays.

Implementation The constructive solid geometry (CSG) is a representation model based on the boolean set operations. A solids in this representation is a result from the applications of boolean set operations on elementary solids, called primitives. Spheres, cones, cylinders and rectangular solids are examples of primitives. The CSG solid representation contains the primitives used and operations applied to create the solid. It is structured as a tree, where each operation is represented as a node, and each primitive as a leaf. It's called CSG tree. 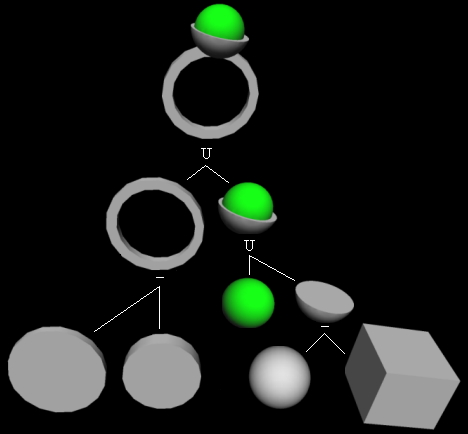To renderize CSG solids, it's recommended to use as internal representation a one that is more suitable for that purpose. When rendering a solid, it's CSG tree must be traversed using a depth-first search algorithm. The nodes are visited in the order that the operations were applied. On each leaf visit, the leaf's primitive is created on the internal representation. On each node visit, the node's boolean set operation is applied on the solids obtained in the child nodes using a proper algorithm for the internal representation. The same operations applied to create the CSG solid are applied, at the same order, on primitives in the internal representation. In the end, the solid in internal representation equivalent to the CSG solid is created and can be used to renderize the solid. The b-rep representation may be used as CSG internal representation, what is a quite robust and flexible approach to represent solids created with boolean set operations. When it is used, the b-rep solid equivalent to a CSG solid is obtained when its renderization is required. But an algorithm to combine b-rep solids with boolean set operations is necessary for this approach to work. One is described at Constructive Solid Geometry for Polyhedral Objects, by D. H. Laidlaw, W. B. Trumbore, and J. F. Hughes. First, the algorithm subdivides the faces of the solids in a way that there isn't faces intersection among them. Then, the faces of a solid are classified based on the surface of the other as being, inside, outside or on its boundary. Depending on how a face was classified and what operation is being applied, it will or will not be included on the new solid. Click here to download an article that detail the subject (in portuguese).

Gallery Boxer images/boxer.jpg Boxer Cup images/cup.jpg Cup Ring images/ring.jpg Ring Pacman images/pacman.jpg Pacman Congresso images/congresso.jpg Congresso Worm images/worm.jpg Worm

Links https://sourceforge.net/projects/graxml/ Geometric Modeller for handling High Energy Physics experiments' Detector Description and Event data.. It uses J3DBool library to apply boolean set operations on 3D elements. http://createuniverses.blogspot.com/2008/09/constructive-solid-geometry-program.html Application to demonstrate an algorithm for performing CSG operations, that is a C++ port of J3DBool library.